A Estereografia nada mais é do que o ato de representar sólidos em um plano. Desse modo, por definição, a Projeção Estereográfica é a projeção de uma esfera em um plano tangente. Sendo assim, é a projeção de elementos planares (foliação, acamamento, falha, fratura e diques). E também, lineares (eixo de dobra ou linha de charneira, intersecção entre planos, estria e lineação de estiramento mineral). Esses são situados no espaço com preservação dos ângulos e de suas relações angulares.
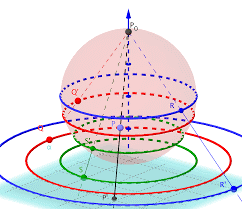
Projeção Estereográfica em Geologia
As aplicações desse estudo em Geologia Estrutural são de extrema importância, principalmente nos campos de Geologia de Petróleo, Geologia de Exploração, Mineração, Geotecnia, Geologia Ambiental, Hidrogeologia, estudos de terremoto e energia geotérmica.
Isso porque, é através dessa projeção que conseguimos obter informações sobre o movimento e captura de fluidos magmáticos. Esses fluidos são altamente influenciados por dobras, falhas e fraturas da crosta terrestre. Assim, o conhecimento sobre a visualização de estruturas geológicas a partir da Projeção Estereográfica, possui grande valor para empresas que possuem um dos seguimentos listados acima, visto que, é a partir das redes estereográficas que podemos avaliar se em um dado local possui um depósito mineral, por exemplo.
Além disso, essa é também uma técnica essencial para Cristalografia, Sismologia e Paleomagnetismo, isto porque a utilização de redes estereográficas é essencial pra uma ampla variedade de atividades que dependem da visualização de estruturas geológicas.
A Projeção Estereográfica e a Cartografia
Uma das aplicações da estereografia é a Cartografia. Com a ferramenta criada vários tipos de mapas podem ser obtidos, como por exemplo o da figura 3. Esta é, por ventura, uma das aplicações mais populares da Projeção Estereográfica.
Assim, dentre as Projeções Cartográficas, podemos criar mais 6 tipos de mapas, que são divididos quanto ao método de construção (projeção geométrica gnomônica, estereográfica e ortográfica) e quanto à superfície de projeção adotada (projeções planas ou azimutais, cônicas e cilíndricas).
Como funciona esse estudo na análise de estruturas geológicas?
As rochas costumam parecer imutáveis aos nossos olhos, mas são na realidade, produtos de processos sedimentares, metamórficos e ígneos. Assim, a projeção estereográfica se torna uma importantíssima ferramenta no estudo da Geologia Estrutural, permitindo a análise de orientações e relações angulares envolvendo diversas estruturas planares e lineares das rochas.
No entanto, é sabido que esta técnica exige a capacidade de desenvolver uma visão tridimensional das estruturas geológicas, observando-se que, com frequência, os estudantes sentem dificuldades para compreender e executar os procedimentos. Visto que, o estudo de projeção estereográfica e da Geologia Estrutural se depara com dois problemas: a carência em familiaridade com direções de compasso e com especificações de planos e orientações lineares e problema com a visualização a qual dificulta a correta compreensão dos princípios e práticas de projeção.
O que é a Esfera riemanniana
A Esfera de Riemann é a projeção estereográfica de uma esfera sobre um plano, sendo que essa projeção seja definida na esfera inteira, exceto no ponto de projeção. A aplicação desta técnica no GeoGebra ao estudo de algumas propriedades da Esfera de Riemann facilita a criação de uma esfera e círculos concêntricos perfeitos, facilitando, assim, o estudo da geologia e das projeções através da visualização gráfica.
Gostou do texto? Confira outros conteúdos em nosso blog e conheça os serviços! Entre em contato conosco por meio de nosso (31) 9 7167-5141, e-mail minasjr@minasjr.com.br ou redes sociais Facebook e Instagram, e veja o que podemos fazer por você!
Autora: Julia Ferrarez